CONCEPTOS DE INTELIGENCIA ARTIFICIAL
La inteligencia artificial (IA) trabaja mediante la combinación de una gran cantidad de datos con un rápido e iterativo procesamiento y el empleo de distintos algoritmos, logrando que un software aprenda automáticamente los patrones o características en que producen el conjunto de los datos. La inteligencia artificial es un extenso campo de estudio que contiene una gran cantidad de teorías, métodos y distintas tecnologías. Los principales subcampos son los siguientes:
El ANS viene del inglés Artificial Neural Systems que traducido significa Redes Neuronales Artificiales (RNA), es decir, las no biológicas aunque tienen su inspiración en ellas.
IA significa inteligencia artificial, y es el tema que nos ocupa en el presente documento.
El aprendizaje máquina automatiza la creación de modelos analíticos. Utiliza una mezcla de métodos de redes neurales (RN), métodos estadísticos, desarrollo de operaciones y física, para hallar el patrón oculto en los datos procesados sin existir un programa desarrollado de manera explícita para que sepa qué hay que buscar y qué obtener.
Una red neural (RN) es un aprendizaje basado en máquina formado por unidades interconectadas (neuronas) que procesa datos procedentes de entradas externas, transmitiendo información entre cada neurona o unidad. El proceso necesita de múltiples intercambios entre los datos para encontrar conexiones y obtener significado o patrón de los datos no definidos.
El aprendizaje profundo o a fondo utiliza enormes redes neurales multinivel, aprovechando los avances en el poder de cómputo y las nuevas técnicas de entrenamiento para buscar patrones complejos en grandes cantidades de datos. En la actualidad existen aplicaciones muy comunes que incluyen el reconocimiento de imágenes y del habla.
El procesamiento cognitivo es un subcampo de la inteligencia artificial (IA) el cual busca la interacción hombre – máquina. Mediante el empleo de la inteligencia artificial (IA) y el cálculo cognitivo, se busca que una máquina simule procesos parecidos a los humanos a través de la capacidad de dilucidar imágenes y palabras, de forma que proporcione una respuesta hablada coherente.
La visión por ordenador se fundamenta en el reconocimiento de patrones y en el aprendizaje profundo para reconocer lo que compone una imagen o un video. Esto permite a los ordenadores, máquinas y dispositivos varios, analizar, procesar, comprender y capturar imágenes o videos en tiempo real además de interpretar el medio que le rodea.
El procesamiento del lenguaje natural (en inglés, Natural Language Processing o NLP) es la habilidad de los ordenadores de analizar, comprender y generar lenguaje humano, como el habla. La posterior etapa del NLP es la interacción en lenguaje natural, permitiendo al ser humano comunicarse con los ordenadores empleando un idioma humano.
Además, distintas tecnologías habilitan y permiten la existencia de la inteligencia artificial:
Las unidades de procesamiento gráfico son elementales para la inteligencia artificial puesto que dan la capacidad de cálculo requerido para el procesamiento iterativo. Entrenar redes neurales requiere de una gran cantidad de datos estructurados (big data), además de un importante poder de cómputo.
El Internet de las Cosas (IoT) genera cantidades ingentes de datos de dispositivos y aparatos interconectados, la mayoría de ellos no analizados. La automatización de modelos mediante el empleo de la inteligencia artificial permite utilizar una mayor parte de ellos.
Novedosos algoritmos avanzados combinan nuevas maneras de analizar un mayor y creciente número de datos con una mayor velocidad en distintos niveles. Este procesamiento inteligente es fundamental para identificar y anticipar eventos extraños, comprender sistemas complejos y optimizar escenarios únicos.
Las APIs (en inglés, Application Programming Interface), son paquetes de código que posibilitan añadir funcionalidades de inteligencia artificial a productos y paquetes computacionales existentes. Son capaces de añadir reconocimiento de imágenes a sistemas de seguridad domésticos y realizar preguntas y responderlas, generar subtítulos y encabezados, o buscar y encontrar patrones en los datos.
En resumen, la inteligencia artificial tiene como objeto proveer de un algoritmo que pueda razonar los inputs que recibe y dar un resultado. La inteligencia artificial en el presente y más en el futuro producirá interacciones parecidas a las humanas y dará soporte a tareas específicas.
REDES NEURONALES
Una red neuronal no es más que un algoritmo matemático que trata de asemejar una herramienta informática a las neuronas del celebro.
Las redes neuronales resultan especialmente adecuadas para llevar a cabo reconocimiento de patrones a fin de identificar y clasificar objetos o señales de voz, visión y control. También se emplean para el modelado y la predicción de series temporales.
Algunos ejemplos de uso de redes neuronales:
- Las compañías eléctricas predicen con precisión la carga de sus redes eléctricas para asegurar y mejorar la eficiencia de sus generadores eléctricos.
- Los cajeros automáticos que podemos encontrar en la calle son capaces de aceptar depósitos bancarios de forma fiable empleando la lectura del número de cuenta y del importe del depósito en un cheque.
- Los patólogos confían en programas de detección de cáncer como guía en el momento de clasificar los tumores como benignos o malignos según la uniformidad de las células, su grosor, su masa, la mitosis, entre otros factores.
Presente y futuro de la Inteligencia artificial (IA)
En la actualidad se están destruyendo miles de puestos de trabajo alrededor del mundo debido a la robotización. Todas las tareas repetitivas u objeto de serlo, son y serán sustituidas por máquinas.
Hoy en día dichos dispositivos no necesariamente contienen una IA, pero cuándo se le aplique, juntamente con un descenso en el precio de adquisición, el impacto en el mercado laboral será negativo.
Uno de los sectores dónde se notará más el impacto de la IA es en el campo (la agricultura). Un robot con una inteligencia artificial capaz de recoger frutas y hortalizas hará completamente innecesaria la mano de obra jornalera. Se está empezando a hablar seriamente de la renta universal básica y de la abolición del trabajo.
Sin embargo, desde el punto de vista de los avances científicos, el futuro es prometedor. La IA amplía los límites de la inteligencia humana. Actualmente la IA es capaz de leer miles de artículos científicos y llegar a conclusiones que a un humano le hubiera sido muy difícil o imposible.
En otros campos como el biomédico, serán muy positivos desde dos puntos de vista: diagnosis y tratamiento. Y además, en algunas disciplinas médicas, se ha demostrado que lo hacen mejor que los humanos.
Qué puede hacer una IA y qué no
La respuesta es sencilla. Básicamente y resumiéndolo muchísimo, una Inteligencia Artificial hace lo que haría una persona o celebro humano. Eso sí, mucho más rápido, no descansa y no cobra por ello. Para entenderlo vamos a utilizar el ejemplo de la lotería: ¿es capaz la IA de predecir el siguiente número de lotería ganadora? La respuesta es clara, en principio no. La inteligencia artificial busca patrones, por lo que la lotería en teoría no tiene ningún patrón. Por lo que, no existe actualmente un modelo capaz de predecirla.
En este ejemplo, tengo mi opinión personal al respecto. Quizás en un futuro muy lejano y con el “big data” de absolutamente todo, es decir, muchísimos datos a disposición de una máquina capaz de analizarlos de forma rápida, exista un remoto patrón para ello.
MODELO DE UNA NEURONA ARTIFICIAL
Llegados a este punto, vamos a definir unos conceptos útiles que ya conocemos pero conviene repasar para comprender bibliografía variada sobre el tema que nos ocupa:
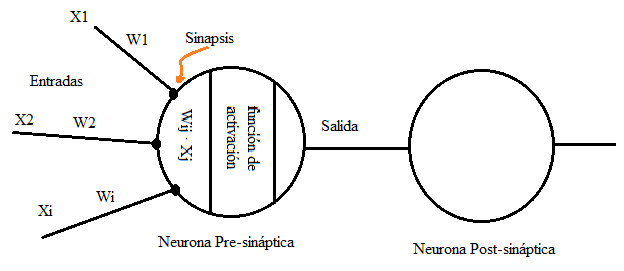
- Entradas: Las variables que entran en el soma y que pueden ser binarias o continuas.
- Pesos sinápticos: La importancia o peso de cada señal.
- Regla de propagación: El producto de los pesos por las entradas o suma ponderada de las entradas con los pesos sinápticos.
- Función de activación: Función que proporciona una determinada señal de salida.
- Neurona presináptica y neurona post sináptica: En el caso de una red neuronal multicapa si considerásemos dos neuronas consecutivas, la presináptica sería la primera y la postsináptica la que recibe señales de la primera.
- Sinapsis inhibidora: Si el peso es negativo la conexión se conoce como inhibidora.
- Sinapsis excitadora: Si el peso es positivo la conexión se conoce como excitadora.
ARQUITECTURA DE LAS REDES NEURONALES
Como hemos indicado, las neuronas se organizan en estructuras o redes conectadas por medio de sinapsis. En estas conexiones, una vez entrenadas, la información fluye en un sentido, de la neurona presináptica a la postsináptica. En general las neuronas se agrupan en capas. Normalmente, en cada capa las neuronas son del mismo tipo. Se pueden distinguir entre tres tipos de capas:
- La capa de entrada: Básicamente son las entradas.
- La capa oculta: Capa en dónde se computan los datos.
- La capa de salida: Proporcionan la salida o respuesta final.
- Conexión intracapa: Son conexiones entre las neuronas de la misma capa.
- Conexión intercapa: Son conexiones entre las neuronas de capas distintas.
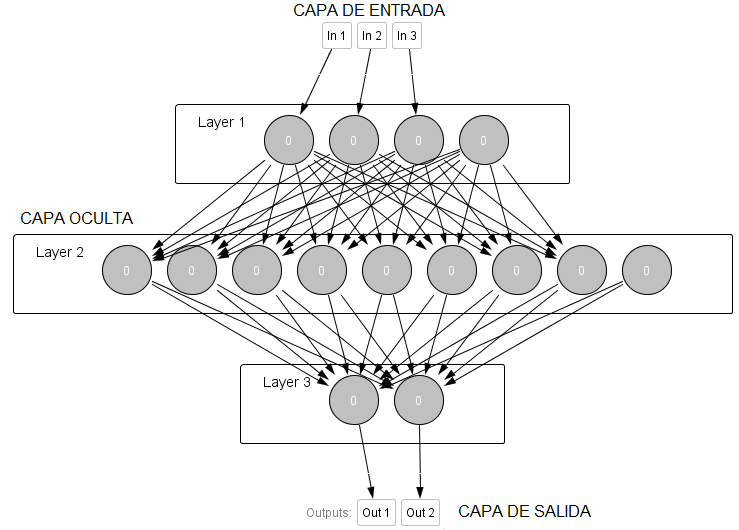
Las redes neuronales pueden ser monocapa, es decir, carece de una capa oculta. Pueden ser multicapa como la de la figura anterior, o recurrente. Este último tipo de red neuronal es algo distinto porque la dirección de la información puede viajar por la misma capa, capas distintas o la misma neurona.
APREDIZAJE DE UNA RED NEURONAL
Hasta ahora hemos hablado de los pesos de la red y de alguna manera los hemos calculado una vez conocido el patrón. Sin embargo, el método numérico que permite el cálculo de estos pesos se denomina aprendizaje de la red. Estos métodos numéricos ajustan los pesos a partir de unos pesos iniciales aleatorios o nulos.
A veces para poder hallar el valor de los pesos es necesaria modificar la estructura de la red, añadiendo nuevas neuronas o eliminándolas, así como añadir nuevas capas de neuronas.
Tipos de aprendizajes
Los tipos de aprendizaje más comunes son el aprendizaje supervisado, no supervisado, híbrido y reforzado.
- Aprendizaje supervisado: Hasta ahora hemos visto brevemente el aprendizaje supervidado. Es decir, aquel que a partir de unas entradas y salidas concretas, deseamos conocer el valor de los pesos. Es decir, conocemos el patrón y unas salidas concretas, y mediante unos métodos numéricos se hallarán unos pesos. Luego veremos alguno.
- Aprendizaje no supervisado o autoorganizado: A partir un patrón, sin unas salidas conocidas, se buscan regularidades en éste, rasgos o agrupaciones según su similitud (conocido como clustering).
- Aprendizaje híbrido: Son varias capas de neuronas dónde conviven el aprendizaje supervisado y el no supervisado.
- Aprendizaje reforzado: No se suministra una salida explícita. Se trata de recompensar o premiar al algoritmo. Se emplea en teoría de juegos, teoría de control, investigación de operaciones o teoría de la información.
Fase de recuerdo
Una vez el sistema ha aprendido, es decir, ha calculado los pesos, estos se quedan fijos en la memoria y se pueden emplear. Es decir, la red ya no aprende pero podemos encontrar dos situaciones:
- En las redes unidireccionales, ante una entrada, obtendremos unas salidas. No hay bucles de retroalimentación.
- Las redes con retroalimentación son sistemas dinámicos no lineales en las que es más complicado obtener un resultado convergente.
LA NEURONA
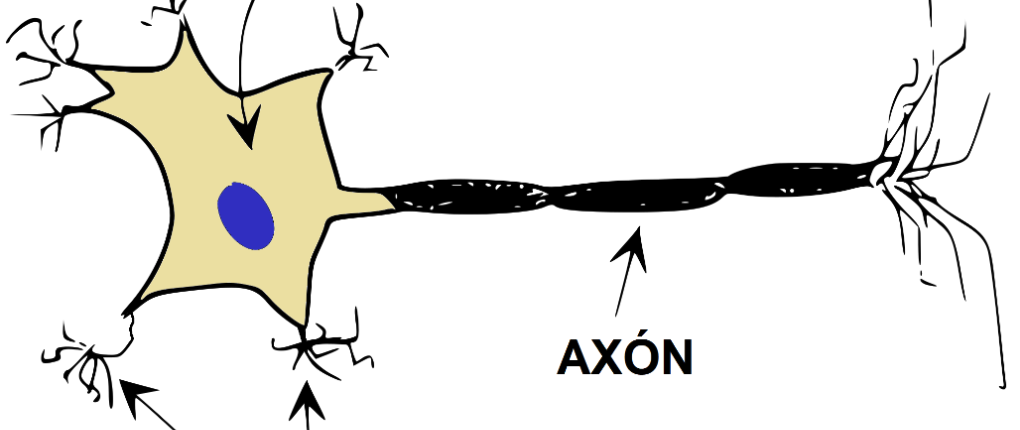
El sistema nervioso de un ser humano, se estima que contiene alrededor de 100.000 millones de neuronas. Éstas están organizadas mediante una compleja red en la que las neuronas individuales pueden estar conectadas a varios miles de neuronas distintas. Se calcula que una neurona del córtex cerebral recibe información, por término medio, de unas diez mil neuronas, y envía impulsos a varios cientos de ellas. Desde un punto de vista funcional, las neuronas se constituyen en simples procesadores de información. Desde que D. Santiago Ramón y Cajal (Navarra) descubriera las neuronas se sabe que toda neurona, posee un canal de entrada de información, las dendritas; un órgano de cómputo, el soma, y un canal de salida, el axón.
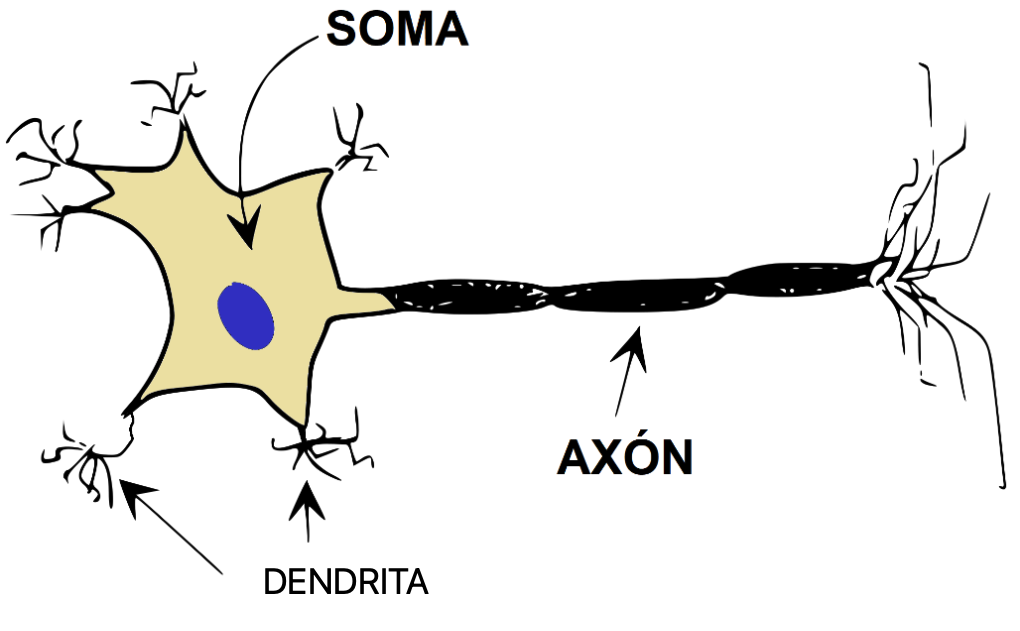
Entonces, en el “soma” se procesará la información que le llega a través de una serie de conexiones (dendritas), multiplicadas por unos pesos (o pesos sinápticos) en la jerga de las redes neuronales. Su nomenclatura es wij. Dónde la “i” es la entrada y “j” es la neurona. Un peso es la importancia que tiene una entrada “i” sobre la neurona “j”. Al final en una neurona biológica se hace una suma de todas las señales (xi) que le llegan, pero cada señal tendrá una intensidad e importancia diferente, es decir, un peso distinto. Esto tiene su lógica, porque habrá sentidos quizás más importantes que la señal procedente de otra neurona.
Es fácil e intuitivo pensar que la salida de una neurona artificial puede ser considerada la entrada de otra neurona para construir así una red neuronal conocido como perceptrón. Esta red neuronal, como mínimo tendrá una neurona de entrada conectada a otra neurona de salida.
Con todo lo anterior es razonable pensar que, de alguna manera una red neuronal es una ponderación:
y1 = W11·X1 + W21·X2 + W31·X3 +····+ Wn1·Xn
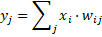
Es decir, una red neuronal podría ser una función de pesos. ¿Pero la anterior expresión es cierta? ¿Cómo se puede comprobar? La forma de hacerlo es mediante las funciones lógicas más simples que existen, NOT, XOR, OR, AND, etc. Si el modelo propuesto vale, es válido para una red neuronal. Es decir, tenemos unas entradas y unas salidas. Por lo que vamos a buscar unos pesos que nos den unos determinados Outputs cuándo tengamos unos determinados Inputs. Veamos:
| TABLA VERDAD PUERTA LÓGICA NOT | |
| X1 | Yj |
| 0 | 1 |
| 1 | 0 |
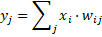
- 1 = 0 · w1j — imposible!
- 0 = 1 · w1j
Ya sólo empezar vemos que el anterior modelo falla, porque claro, cero por algo no da nunca uno. Entonces, cómo el modelo puro de ponderación falla, se añade una modificación que lo mejora. Se añade lo que se denomina por “bias” o “conexión a masa”. Éste es un término inglés que se traduciría por «sesgo» y no existe en la actualidad tal palabra en la Real Academia Española de la Lengua, por lo que no lleva acento. Veamos:
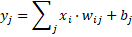
Entonces, vemos que lo anterior es la expresión de una recta. La “bia” o “conexión a masa” es constante para cada neurona. A la bia también se la denota por “θ”. Al sumatorio de cada una de las entradas por su peso se le suele llamar por “neta”. Entonces, vamos a intentarlo de nuevo:
- 1 = bj + 0 · w1j
- 0 = bj + 1 · w1j
Si resolvemos el sistema de ecuaciones tendremos bj = 1 y w1j = -1. Ahora parece que el sistema funciona. Vamos a ver si funciona para una OR.
| TABLA VERDAD PUERTA LÓGICA OR | ||
| X1 | X2 | Yj |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Pero aquí tengo un problema. Veamos, con una neurona tenemos la siguiente expresión:
- y1 =b1 + x1·w11 + x2·w21 — b1 + 0·w11 + 0·w21 = 0 — b1 = 0
- y1 =b1 + x1·w11 + x2·w21 — b1 + 0·w11 + 1·w21 = 1 — w21 = 1
- y1 =b1 + x1·w11 + x2·w21 — b1 + 1·w11 + 0·w21 = 1 — w11 = 1
- y1 =b1 + x1·w11 + x2·w21 — b1 + 1·w11 + 1·w21 = 1 — IMPOSIBLE
Con la anterior ecuación y estructura es imposible encontrar las incógnitas porque no se cumple el último caso. Además, si tenemos tres ecuaciones para que el sistema sea determinado debe haber tres incógnitas. Quizás puede ser un tema de estructura, con una neurona no es posible. Vamos a probarlo añadiendo otra neurona “inventada”. Veamos:
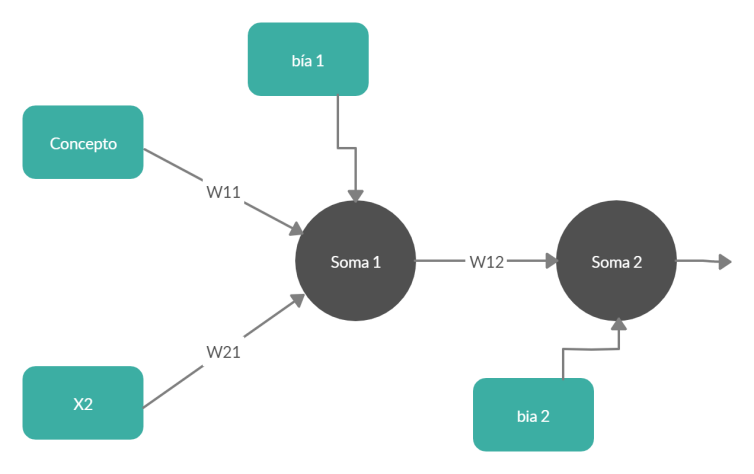
Pero añadiendo una neurona más faltaría otra ecuación. Así que la red de la figura 2 no es válida. Probemos en cambiar la estructura completamente. Veamos:
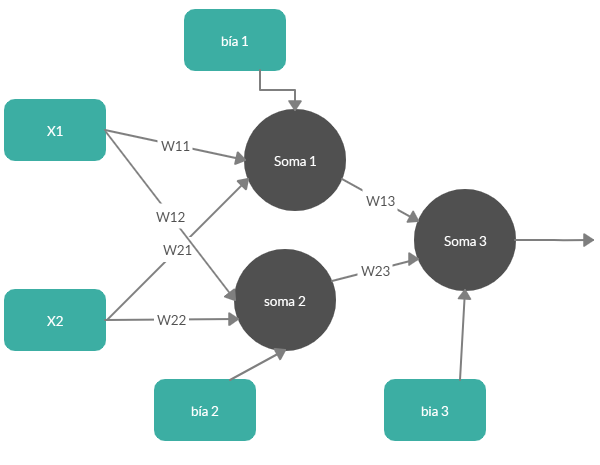
- y1 = b1 + x1 ·w11 + x2·w21
- y2 = b2 + x1· w12 + x2·w22
- y3 = b3 + y1· w13 + y2·w23
Aquí se plantean tres ecuaciones y nueve incógnitas. Al ser el número de incógnitas superior al de ecuaciones el sistema puede ser compatible indeterminado o incompatible, pero nunca determinado. Veamos:
Llegando a la siguiente ecuación: y3 = b3 + w13 · (b1 + x1 ·w11 + x2·w21)+ w23·(b2 + x1· w12 + x2·w22)
Probamos:
- y3 = b3 + w13 · (b1 + 0 ·w11 + 0·w21)+ w23 · (b2 + 0· w12 +0·w22) = b3 + w13 · b1 + w23· b2 = 0
- y3 = b3 + w13 · (b1 + 0 ·w11 + 1·w21)+ w23·(b2 + 0· w12 + 1·w22) = b3 + w13 · (b1 + w21) + w23·(b2 + w22) = 1
- y3 = b3 + w13 · (b1 + 1·w11 + 0 ·w21)+ w23·(b2 + 1· w12 + 0·w22) = b3 + w13 · (b1 + w11) + w23·(b2 + w12) = 1
- y3 = b3 + w13 · (b1 + 1 ·w11 + 1·w21)+ w23·(b2 + 1· w12 + 1·w22) = 1
Entonces, tenemos:
- b3 + w13 · b1 + w23· b2 = 0
- b3 + w13 · (b1 + w21) + w23·(b2 + w22) = 1
- b3 + w13 · (b1 + w11) + w23·(b2 + w12) = 1
- b3 + w13 · (b1 + w11 + w21) + w23·(b2 + w12 + w22) = 1
Tengo cuatro ecuaciones y las siguientes incógnitas: b3, w13 , b1 , w11 , w21, w23, b2, w12, w22
b3 = – w13 · b1 – w23· b2
Si sustituimos la anterior ecuación en la segunda, tercera y cuarta:
– w13 · b1 – w23· b2 + w13 · (b1 + w21) + w23·(b2 + w22) = 1
Quedando:
w13·w21 + w23·w22 = 1
Luego, para la tercera ecuación:
– w13 · b1 – w23· b2 + w13 · (b1 + w11) + w23·(b2 + w12) = 1
Esto es igual a:
w13·w11 + w23·w12 = 1
Finalmente, en la última ecuación:
– w13 · b1 – w23· b2 + w13 · (b1 + w11 + w21) + w23·(b2 + w12 + w22) = 1
Esto es igual a:
w13·w11 + w13·w21 + w23·w12 + w23·w22 = 1
Si lo reorganizamos veremos que:
w13·w11 + w23·w12 + w13·w21 + w23·w22 = 2
Pero debería dar 1. Por lo que 2 no es igual a 1. Esto significa que el sistema no se puede resolver. Al final llegamos a la conclusión que el problema no es de estructura (o arquitectura) sino de modelo.
INTRODUCCIÓN AL PERCEPTRON
Conociendo lo anterior y viendo que una simple ponderación no es suficiente para todos los casos, independientemente de la estructura, llegamos a la ecuación y modelo de lo que se conoce por perceptrón:
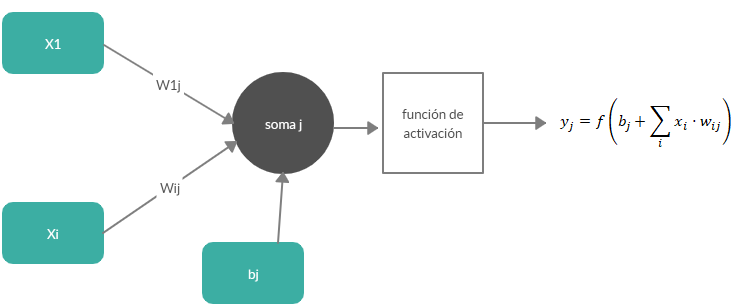
Hasta ahora, hemos visto que una ponderación no es suficiente. Para mejorarlo hemos añadido el concepto de «bias». Y cómo esto no es suficiente hemos variado la estructura sin demasiado éxito. Pero la idea de fondo no es incorrecta. El Perceptrón añade al producto de los pesos por las entradas más las «bias», el concepto de “función de activación”. Esta función de activación del Perceptrón es una función que recoge el resultado y si es mayor de un determinado valor (o umbral) el resultado es uno, sino cero.
La función de activación antes descrita se la conoce por STEP, o función escalón. Hay más tipos de funciones de activación que veremos posteriormente aplicables a otro tipo de redes neuronales.
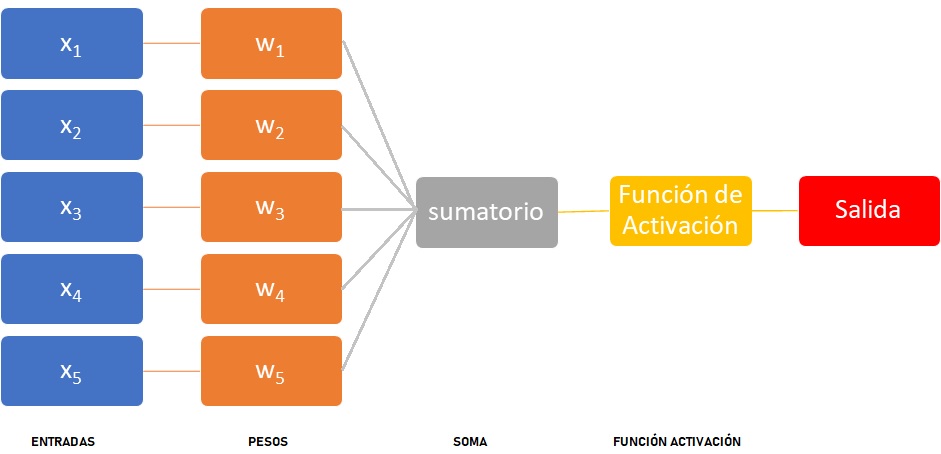
Características del Perceptrón:
- El Perceptrón se aplica sólo a problemas linealmente separables. Esto se debe a que la función de activación que lleva de por sí el Perceptrón no es derivable.
- Cada neurona del Perceptrón lleva después del SOMA su función de activación STEP.
- Los perceptrones pueden ser de una sola neurona o tener varias neuronas con lo que se conoce Perceptrón Multicapa.
- El Perceptrón sólo da resultados binarios, es decir, debido al tipo de función de activación que emplea, sólo puede dar resultados cero (o -1) y uno, pero nunca dará como resultado un decimal. La función STEP básicamente es un pasa o no pasa, es decir, es un alto o es un bajo.
La función de activación “STEP”
La función “step” convierte la señal ponderada en 0 ó 1 de la siguiente forma: la señal después de la unión sumadora es 0 si X ≤ 0 y es 1 si X > 0.
Por ejemplo:
- STEP(-453) = 0
- STEP (-1) = 0
- STEP(23) = 1
- STEP(2) = 1
Pero a veces el umbral no es el 0. Puede ser otro valor. Es decir, podemos elegir el umbral. Por ejemplo, el 5:
- STEP(-4) = 0
- STEP (-1) = 0
- STEP(6) = 1
- STEP(7) = 1
Puerta lógica NOT
Vamos ahora a probar con la primera puerta con la que hemos empezado el libro. La puerta lógica NOT.
| TABLA VERDAD PUERTA LÓGICA NOT | |
| X1 | Yj |
| 0 | 1 |
| 1 | 0 |
Si repasamos el caso que ya habíamos hecho, tenemos:
- 1 = b1 + 0·w1
- 0 = b1 + 1·w1
Es decir, bj = 1 y w1j = -1. Añadiendo la nueva función:
- Y = step (b1 + x1·w1) = step (1 + 0 · (-1)) = step (1) = 1
- Y = step (b1 + x1·w1) = step (1 + 1 · (-1)) = step (0) = 0
Por lo que lo anterior se cumple perfectamente. Lo que pasa es que aquí ya conocíamos los datos más importantes, pero no siempre es así. Veamos los siguiente casos para aprender cómo se consiguen todos los parámetros.
Puerta lógica OR
Para encontrarlos vamos a comprobar la “Or”. Veamos:
| TABLA VERDAD PUERTA LÓGICA OR | ||
| X1 | X2 | Yj |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
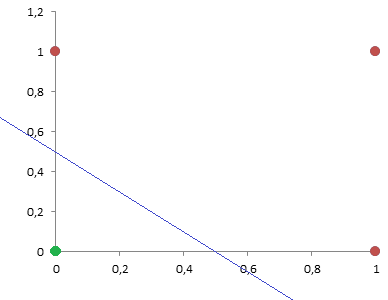
El problema está en que ¿cómo hallamos los pesos y las bias? La solución está en representar la anterior tabla de la verdad (x1 y x2) y colorear en rojo los puntos que tienen como resultado 1 y en verde los puntos que tienen como resultado 0. Luego trazamos una línea, también denominado “hiperplano”, que los separe. Es decir, una línea divisoria entre el mundo rojo y verde.
El motivo es que si nos fijamos en lo que hay dentro del STEP veremos que es una recta de toda la vida:
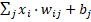
Es decir una recta del tipo y = mx + b que pasa por los puntos p1 = (0, 0.5) y p2 = (0.5, 0)
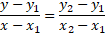
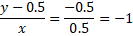
y – 0.5 = -x, entonces la «y» será igual a: y = -x + 0.5
Lo que traducido a x1 y x2, es: x1 + x2 – 0.5 = 0. Es decir, w11 = 1, w21 = 1 y b1 = -0,5. Vamos a probar si es cierto:
Y = STEP (x1 + x2 – 0.5)
Si probamos:
- Y = STEP (0 + 0 – 0.5) = 0 OK
- Y = STEP (0 + 1 – 0.5) = 1 OK
- Y = STEP (1 + 0 – 0.5) = 1 OK
- Y = STEP (1 + 1 – 0.5) = 1 OK
Por lo tanto, se cumple en todos los casos.
El tema es que hay que buscar una o varias RECTAS que separe un patrón. Esto es lo que define al perceptrón, es decir, que los datos son linealmente separables.
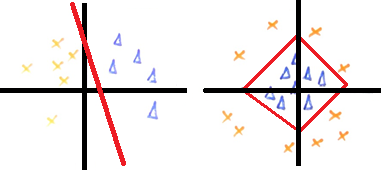
En el ejemplo superior izquierdo, los datos se pueden separar con RECTAS, sin embargo, es más complejo en el izquierdo, puesto que se podría aislaría con un pentágono, hexágono, etc. Por lo que perceptrón se puede aplicar en ambas figuras, siempre que se usen rectas. Otro detalle, es que cuando sea necesario emplear rectas para separar regiones, estamos hablando de añadir capas de neuronas.
Puerta lógica AND
La puerta AND es aquella que devuelve un ‘0’ si alguna de sus entradas es ‘0’ y devuelve un ‘1’ si sus dos entradas son ‘1’.
| X1 | X2 | Y1 |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Lo que realizará nuestra red neuronal va a ser dividir en dos planos las soluciones (ver siguiente imagen). Lo que «caiga» en un lado del plano dará como salida un ‘0’ y lo que caiga al otro lado dará como salida un ‘1’.
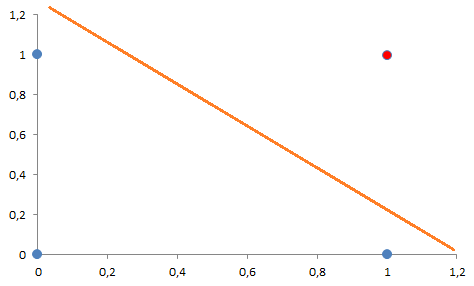
Calculamos la recta:
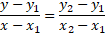
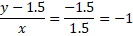
X1+ X2 – 1.5 = 0
Analizamos todos los casos con la función STEP y vemos que sucede:
- Y = STEP(X1+ X2 – 1.5) = STEP(0 + 0 – 1.5) = 0
- Y = STEP(X1+ X2 – 1.5) = STEP(1 + 0 – 1.5) = 0
- Y = STEP(X1+ X2 – 1.5) = STEP(0 + 1 – 1.5) = 0
- Y = STEP(X1+ X2 – 1.5) = STEP(1 + 1 – 1.5) = 1
Luego vemos que tanto la estructura como el modelo, se cumple perfectamente.
Puerta lógica XOR
Analicemos que sucede con la XOR. Su tabla de la verdad es la siguiente:
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Al representar X1 y X2 vemos que no parece evidente la división de valores. Pero realmente no es un problema, esto sucede cuando tenemos más de una neurona. La manera de solucionarlo es la misma que hemos estudiado anteriormente. Es decir, calculamos ambas ecuaciones y luego analizamos lo que sucede:
Primera ecuación para los puntos, p1 = (0, 0.5) y p2 = (0.5, 0).
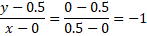
Y = -x + 0.5 Es decir: X1 + X2 – 0.5 = 0 b1 = -0,5. w11 = 1. w21 = 1.
A segunda ecuación contiene los puntos, p3 = (0, 1.5) y p4 = (1.5, 0):
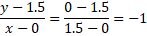
Y = -x + 1.5 y cómo X1 + X2 -1.5 = 0 además, b2 = -1.5. w12 = 1, w22 = 1.
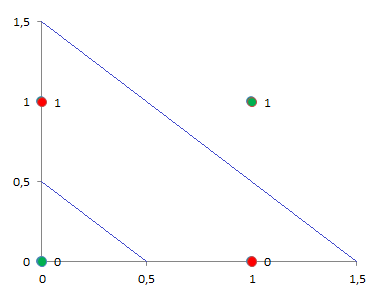
Luego, para ambas ecuaciones aplicamos perceptrón:
- Y = STEP (X1 + X2 – 0.5)
- Y = STEP (X1 + X2 – 1.5)
Damos valores para la primera ecuación “a”:
- Y1 = STEP (0 + 0 – 0.5) = 0
- Y1 = STEP (0 + 1 – 0.5) = 1
- Y1 = STEP (1 + 0 – 0.5) = 1
- Y1 = STEP (1 + 1 – 0.5) = 1
Damos valores para la primera ecuación “b”:
- Y2 = STEP (0 + 0 – 1.5) = 0
- Y2 = STEP (0 + 1 – 1.5) = 0
- Y2 = STEP (1 + 0 – 1.5) = 0
- Y2 = STEP (1 + 1 – 1.5) = 1
¿Qué es lo que hemos hecho? Pues un Perceptrón Simple de dos neuronas, en dónde cada línea es una neurona. Ahora hemos de juntar los resultados anteriores. Lo hacemos creando una tabla de la verdad nueva, con Y1 e Y2. Veamos:
| X1 | X2 | Y1 | Y2 | Y3 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Esto si lo representamos conseguimos una ecuación Y2 – Y1 – 0,5 = 0. Es decir, Y3 = STEP (Y2 – Y1 – 0,5 ). Por lo que ya tenemos la red neuronal completa definida en tres expresiones.
- Y1 = STEP (X1 + X2 – 0.5)
- Y2 = STEP (X1 + X2 – 1.5)
- Y3 = STEP (Y2 – Y1 – 0,5)
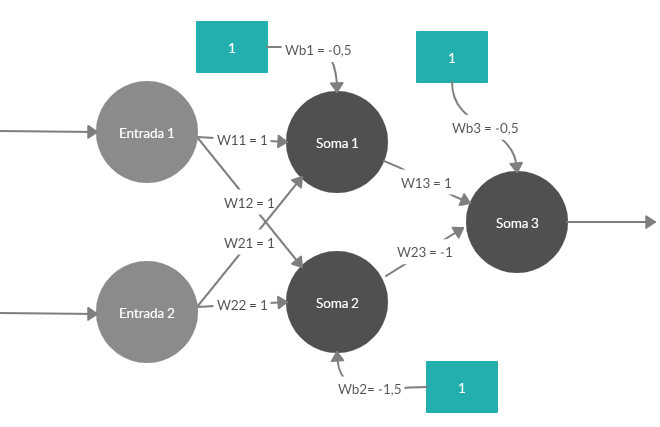
Con lo anterior hemos visto que la función XOR no puede ser aprendida por un único Perceptrón o neurona puesto que requiere de dos funciones lineales para separar los distintos valores.
RESOLUCIÓN NUMÉRICA DE LOS PESOS DEL PERCEPTRÓN
El Perceptrón Simple (Rosenblatt, 1959), está formado de una única neurona con “n” entradas y una salida, además sólo utiliza señales binarias. El perceptrón simple en empleado únicamente para clasificar problemas linealmente separables, cosa se puede realizar empleando métodos estadísticos, y de forma más eficiente. La información viaja unidireccionalmente.
A continuación, mediante un ejemplo se explicará el proceso de aprendizaje del Perceptrón. Para el ejemplo se empleará la siguiente tabla de la verdad correspondiente al OR:
| X0 | X1 | X2 | Z |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 |
Al final lo que se desea es que para unas determinadas entradas haya unas determinadas salidas. Esto es lo que se conoce cómo el aprendizaje supervisado. El proceso consiste en mostrarle al perceptrón las entradas y las salidas correctas para esas entradas. Para realizar el proceso de aprendizaje artificial el Perceptrón inicia con pesos aleatorios, sin embargo, más adelante veremos que hay unas recomendaciones a seguir. Por último y antes de empezar con el proceso, usaremos la siguiente expresión para actualizar los pesos que permitirá encontrar alternativas que puedan aprender y arrojar las salidas correctas a las entradas. La regla de aprendizaje es una variante de la conocida ley de Hebb:
Wj+1 = Wj + η · e · Xj
- Wj+1 = Peso nuevo
- Wj = Peso actual
- η = Tasa o factor de aprendizaje
- e = error
- Xj = Entrada
La tasa de aprendizaje amortigua el cambio de los valores de los pesos, su valor va de 0 a 1. La tasa o el llamado factor de aprendizaje es una constante empírica que determina la facilidad con la que la red es capaz de aprender.
Recordemos que el perceptrón simple no podrá con todo, por ejemplo y sin ir muy lejos con una tabla XOR.
Ejemplo con una iteración
Pero a modo de ejemplo, imaginemos que tenemos los siguientes pesos y «bias» iniciales. Vamos a ver qué sucede. W0 = 1, W1 = 1, W2 = 0, Wb = 1, bias = -0,8. Tasa de aprendizaje = 0,5 y umbral = 0.

Primera fila
Z =STEP(X0·W0 + X1·W1 + W2·b2) = STEP (1·0 + 1·0 –1· 0.8) = -0.8 ≤ 0 –> Activación –> Z = 0
e = activación – Z = 0 – 0 = 0
Corrección = e·η = 0
Por lo que los nuevos pesos son iguales a los iniciales. En las demás filas sucede lo mismo. No hacen falta nuevas iteraciones.
Ejemplo con ocho iteraciones bias nulo, cuatro entradas y tres muestras
Vamos a plantear otro ejemplo de tres entradas y cuatro muestras con un umbral de 0.5. Observen que el umbral no tiene por qué ser igual a 1. El valor de las bias es igual a 0, es decir, no hay bias. Entonces como datos iniciales:
- W1 = 0, W2 = 0, W3 = 0
- bias = 0 y Wb = 0.
- Aprendizaje, η = 0,1
- Umbral = 0,5

Ejemplo de dos iteraciones y bias no nulo
Veamos otro ejemplo con los tres parámetros, es decir, bias igual a 1, tasa de aprendizaje igual a 0,9 y un umbra de 0. En este último caso, mayor que 0 es uno y menor que 0 es 0.
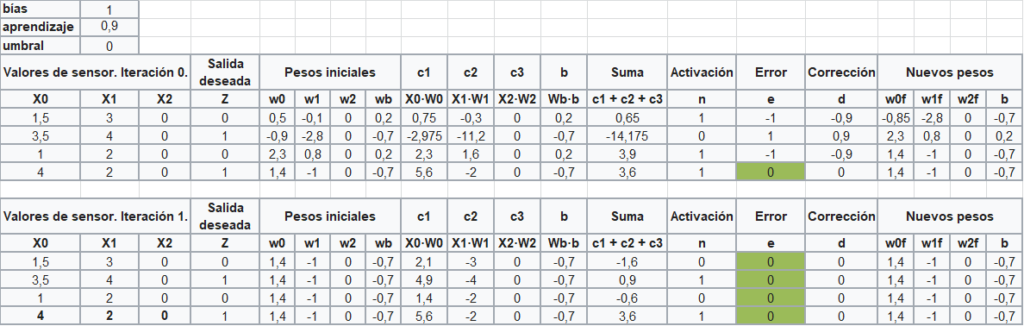
Con este último ejercicio hemos comprendido cuál es la sistemática de un perceptrón simple con una función de activación del tipo STEP.
Como se observa, los pesos finales de cada iteración se convierten en los pesos iniciales de la siguiente iteración.
ADALINE
Una evolución del Perceptrón es ADALINE, Adaptative Linear Neuron. Se parece muchísimo al Perceptrón lo que aquí cambia es la forma de recalcular los pesos.
En 1960 Bernard Widrow y Marcian Hoff publicaron un artículo científico llamado “An Adaptative “Adaline” Neuron using chemical “memistors””. En ese momento usaron circuitos resistivos con memoria permitiendo que el sistema pudiera aprender automáticamente.
La diferencia más grande que existe con el modelo del Perceptrón, es que mientras en éste, la función de activación era una función escalón (0 o 1), en Adaline la función de activación es una función del tipo lineal.
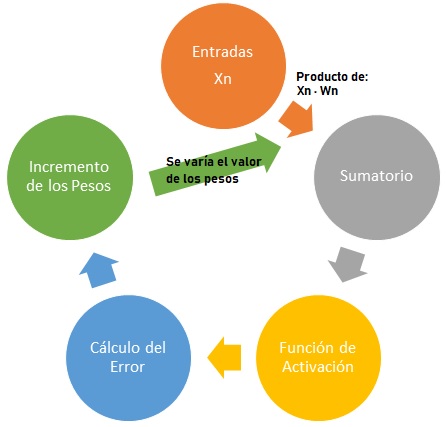
Los pesos de las bias siempre son uno (veremos que en el MADAINE, el peso de sus bias también es uno). ADALINE sólo resuelve, al igual que el Perceptrón, problemas linealmente separables.
La formulación, inicialmente es muy parecida. Veamos que sucede con cada peso:
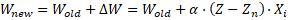
Y el peso de las bias:
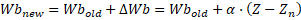
En donde α es la tasa de aprendizaje. Hasta ahora todo es igual que el perceptrón. Pero aquí es cuando se produce la diferencia.
En perceptrón: En el perceptrón, una vez calculados los nuevos pesos para cada fila del patrón, se procedía a realizar el “net” o Zn (columna suma) y luego se procedía con la función de activación “Step”. Si el resultado era igual que el esperado se terminaban las iteraciones.
En Adaline: Se calculan los nuevos pesos para cada fila de la iteración, se procede a realizar el “net” o Zn y luego se calcula para cada fila la siguiente diferencia cuadrada.
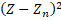
La suma de cada una de las diferencias cuadradas se conoce por el error. Esta función mide numéricamente la diferencia existente entre la salida ofrecida por la red y la salida esperada o correcta.
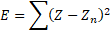
A veces se emplea el error cuadrático medio:
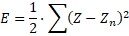
Este error hay que sumarlo en cada iteración y crear una tabla parecida a esta:
| ITERACIÓN | ERROR |
| 1 | 1,51054375 |
| 2 | 0,96922331 |
| 3 | 0,77465163 |
| 4 | 0,70875541 |
| 5 | 0,68911268 |
| 6 | 0,68513677 |
Cuando el error sea mínimo o no varíe significativamente después de algunas iteraciones nos quedaremos con esos pesos.
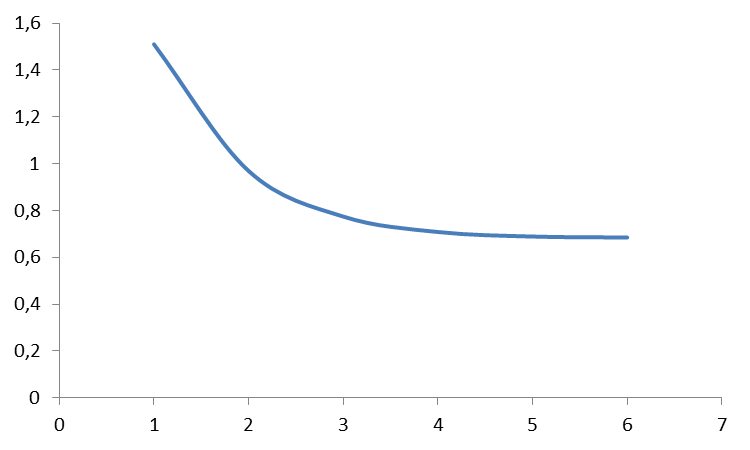
Cuándo hablamos del error en ADALINE hablamos de un valor mínimo. Es decir, aquel por el cual, más abajo no se puede ir, sino lo contrario, subirá. Esto es porque la gráfica del error de ADALINE es un hiperparaboloide que pose o un mínimo global o una recta de infinitos mínimos globales.
Ejemplo ADALINE
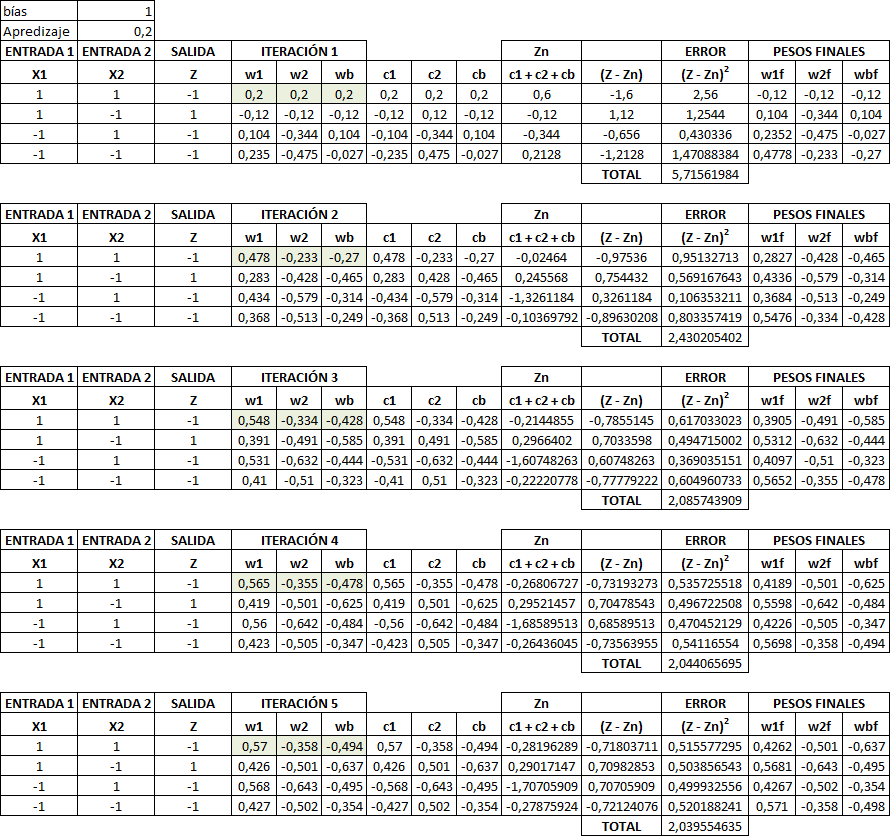
Vamos a poner un ejemplo de Adaline para una neurona. Vamos a realizar cinco iteraciones con una bias de 1 y un aprendizaje de 0,2. Vamos a buscar los pesos para dos entradas. Los pesos iniciales son W1 = W2 = Wb = 0,1.
| X1 | X2 | Z |
| 1 | 1 | 1 |
| 1 | -1 | 1 |
| -1 | 1 | 1 |
| -1 | -1 | -1 |
Aunque se representa en distintos esquemas que podemos encontrar en bibliografía variada, la función de activación en el caso de ADALINE es la identidad. Es decir, no existe una función de activación tipo STEP o SIGMOIDE.
Aplicaciones de ADALINE
Adaline se suele aplicar para filtrar o reducir el ruido de las señales de transmisión de información. También es práctico para filtros adaptativos. En este último caso, ADALINE puede predecir el valor de una señal en t + 1 si conoce el valor de la señal en el instante anterior. ADALINE es capaz de proporcionar predicciones muy exactas.
MADALINE
Manaline viene del inglés Many-Adaline, es decir, muchos Adalines. Está formada por tres capas: la de entrada de datos, la oculta y la de salida. La información fluye unidireccionalmente con origen en las entradas y como fin las salidas. Tiene sólo la función de activación signo. Es decir, si es menor que 0, es igual a -1. Si es igual a 0 es cero. Y si es mayor que cero es +1. Este tipo de función no es derivable porque no es continua.
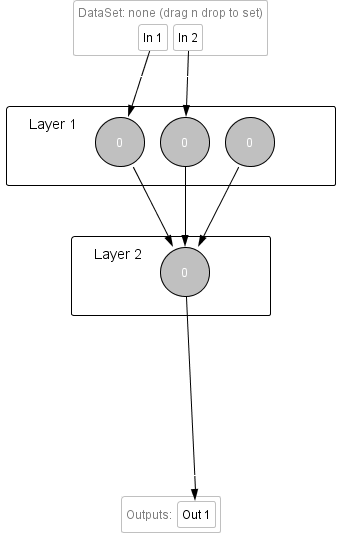
En una red MADALINE la capa oculta contiene un mínimo de tantas neuronas como entradas haya más las bias y sólo existe una única salida. La primera capa es la capa de entradas, la segunda se conoce por el nombre de capa ADALINE y la tercera capa de la conoce por capa MADALINE.
La arquitectura del MADALINE es de flujo hacia adelante. Su función de activación última es la función de signo.
Cálculo de los pesos en una red neuronal del tipo MADALINE
Históricamente se han sugerido tres algoritmos de entrenamiento diferentes para este tipo de redes. Dichos algoritmos se les conoce por la Regla I, Regla II y Regla III.
Regla I de MADALINE (RMI): Esta regla se remonta a 1962. El método de cálculo sólo permite modificar los pesos de la capa oculta pero no la de salida.
Regla II de MADALINE (MRII): el segundo algoritmo de entrenamiento de la red mejoró la anterior Regla I y se describió en 1988. El algoritmo de entrenamiento de la Regla II se basa en un principio llamado de «perturbación mínima«. El proceso se repitepara cada ejemplo haciendo lo siguiente:
- Busca la unidad para la capa oculta (clasificador ADALINE) con la menor confianza en su predicción
- Voltea tentativamente el signo de la unidad.
- Acepta o rechaza el cambio en función de si se reduce el error de la red.
- Se detiene cuando el error es cero.
Regla III MADALINE (MRIII): – La tercera «Regla» aplicada a una red modificada con funciones de activación sigmoideas en lugar de la función de activación signo. Posteriormente se descubrió que era equivalente a la retropropagación.
Además, cuando voltear los signos de unidades individuales no lleva el error a cero para un ejemplo en particular, el algoritmo de entrenamiento comienza a voltear pares de signos de unidades, luego triples de unidades, etc.
FUNCIÓN DE ACTIVACIÓN
La función de activación, representa la activación de umbral existente en las neuronas de los seres humanos. La función de activación, recibe la combinación de los pesos por las entradas a la neurona. Hasta ahora hemos usado la función STEP. Pero muy a menudo se emplean otras funciones, sobre todo cuando interesan respuestas suaves. Es decir, que sean derivables.
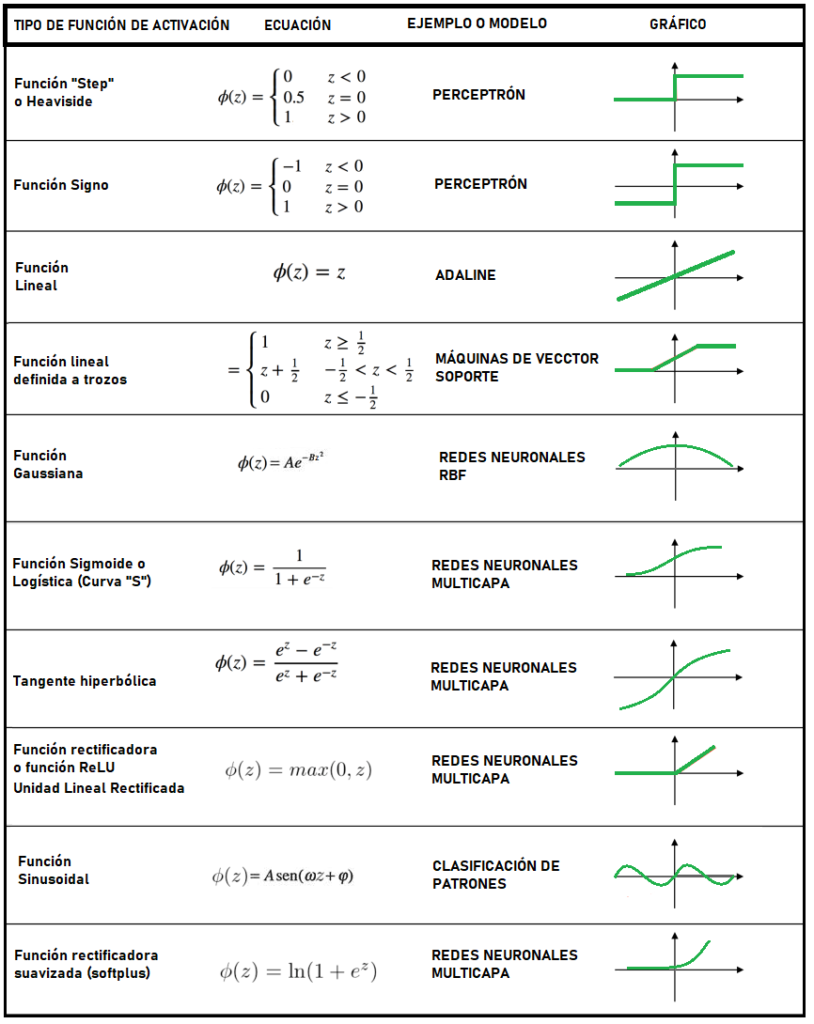
Todas las anteriores funciones tienen sus inconvenientes. Luego son computacionalmente son costosas. Puede ser interesante para las capas ocultas usar un determinado tipo de función de activación o dependiendo de los patrones, es interesante usar otras.
La función tangente hiperbólica
La función tangente hiperbólica tiene respuesta en el rango entre 1 y -1, con asíntotas tendientes hacia estos valores. Es así, como el modelo del perceptrón representa la base del aprendizaje de máquina o aprendizaje automático. No está demás afirmar que los avances en este campo, son gracias a los “simples” percetrones que únicamente aprendían de funciones linealmente separables.
La función de activación sigmoide
La función de activación sigmoide o logística (también llamada curva “S”) es una función muy empleada en redes neuronales. La función pasa exactamente por el valor de 0.5 en el eje de las Y. El resto de la función va desde aproximadamente 0 hasta casi 1. Es decir, sus asíntotas van desde cero a uno.
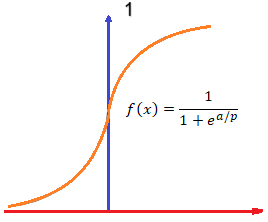
Dónde “e” representa el valor de 2.7183…, luego “p” representa la forma de esta función que en general se deja como “1”. Luego, “a” es el valor resultante de la suma de las multiplicaciones de los pesos por las entradas de las neuronas. Es decir:
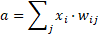
En lenguajes java, “a” se calcularía con un código como el que sigue:
public void activation(){
double addition = 0
for (int i = 0; i < imputs.length; i++){
addition += inputs[i]* weigth[i];
}
activationu = sigmoide.function(addition);
fullInputs();
}
EL PERCEPTRÓN MULTICAPA Y EL BACKPROPAGATION (RETROPROPAGACIÓN)
El Perceptrón Multicapa (MLP) es una extensión y generalización del perceptrón simple en el que:
- Se añaden una o más capas ocultas.
- Se permiten entradas continuas. Es decir, no es necesario restringirse a 0 y 1.
- Las funciones de activación son de tipo sigmoide aunque se pueden emplear otras.
Su principal aportación y mejora es su algoritmo de aprendizaje, también llamado algoritmo de retropropagación (en inglés backpropagation o BP) gracias a Werbos, Rumelhart y Parker.
Cómo hemos visto anteriormente, en la realidad muchas funciones no son linealmente separables (al menos mediante una línea) y en el mundo real no siempre trabajamos con binario, por lo que un Perceptrón simple es un modelo muy limitado. En esto casos el Perceptrón se encuentra fuera de su alcance o poder de aprendizaje artificial. Para lograr dicho aprendizaje, se requiere alguna herramienta más elaborada. Para alcanzar el objetivo de demostrar que las máquinas pueden aprender funciones no linealmente separables, se crea el modelo multicapa. El perceptrón multicapa está compuesto de tres partes: la capa de entrada, la capa oculta y la capa de salida. La capa oculta y la capa de salida están compuestas por nodos o neuronas artificiales. Cada capa está conectada, como antes, por pesos “w”. Esta nomenclatura viene del inglés “weight”.
Es evidente, que tanto las capas ocultas y de salida pueden tener más de un nodo (o neurona). Del mismo modo que hacíamos con el perceptrón simple, el perceptrón multicapa aprende modificando sus pesos. Y al igual que entonces, necesitamos conocer las entradas y salidas correctas. Con esto, el algoritmo puede realizar los cálculos adecuadamente. Pero además, en el perceptrón multicapa se requiere “sincronizar” varias capas con varias neuronas. Para esto se debe de realizar un proceso de aprendizaje que involucre a todas las capas y sus nodos. Existen varios algoritmos para el aprendizaje del Perceptrón multicapa, aquí sólo se analiza el de Backpropagation o retro-propagación.
Se empieza calculando el error en los nodos de salida. Con el error calculado se actualizan los pesos existentes entre la capa de salida y la capa oculta. Seguidamente se calcula el error en las neuronas de la capa oculta, con ayuda de los pesos calculados anteriormente. El siguiente paso consiste en actualizar los pesos existentes entre la capa oculta y la capa de entrada. Después de estos procedimientos se realizan los cálculos desde la capa de entrada hacia la salida verificando que lo recalculado arroje los calores correctos. Este proceso se repite hasta que la re-calcule todas las salidas y estas sean iguales a las salidas deseadas.
Tipos de back propagation
Hay varios tipos de Back-Propagation. Las más comunes tanto en distintos software como en la bibliografía son:
- Sin momentum
- Con momentum
- Resilient propagation
- Dynamic backropagation
Back-Propagation clásico sin momentum
Para entender el procedimiento de back-propagation vamos a analizar el siguiente caso de dos entradas, dos neuronas ocultas y dos salidas. Este magnífico ejemplo lo ha realizado Matt Mazur que se denomina: A Step by Step Backpropagation Example. Además existen “bias” para las neuronas ocultas y de salida. La estructura es la siguiente:
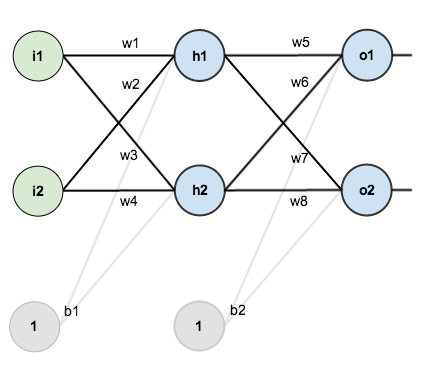
Inicialmente tenemos los siguientes valores de pesos, bias y valores de entrenamiento de entrada y salida. Es decir, en azul tenemos los valores que ante una determinada entrada, habrá una determinada salida. En otras palabras, dadas las entradas 0.05 y 0.10 nosotros deseamos una salida de 0.01 y 0.99.
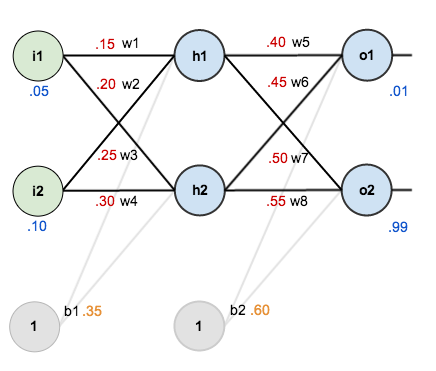
La meta del backpropagation es optimizar los pesos para que la red neuronal pueda aprender como mapear correctamente las entradas y las salidas.
Primero, el paso hacia delante
Para empezar vamos a ver que predice la red neuronal con los pesos y «bias» dados, es decir con las entradas de 0.05 y 0.1. Nosotros averiguaremos la ponderación, llamada en la jerga neuronal “net”, de cada neurona de la capa oculta y luego este resultado lo meteremos dentro de la función de activación, llamada sigmoide o logística, repitiendo el proceso para las capas de salida.
Neth1 = w1·X1 + w2·X2 + b1·1 = 0.15·0.05 + 0.2·0.1 + 0.35·1 = 0.3775
Neth2 = w2·X1 + w4·X2 + b1·1 = 0.2·0.05 + 0.3·0.1 + 0.35·1 = 0,390
Ahora vamos a aplicar la función de activación Sigmoide:
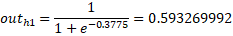
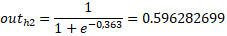
Cómo tenemos las nuevas salidas, ahora vamos a repetir el mismo proceso para la capa oculta.
Neto1 = w5·(outh1) + w6·(outh2) + b2·1 = 0,4·0.593269992 + 0.45·0.59628299 + 0.6 = 1,105635342
Neto2 = w7·(outh1) + w8·(outh2) + b2·1 = 0.5·0.593269992 + 0.55·0.59628299 + 0.6 = 1,224590641
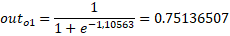
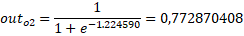
Cálculo del error total
Ahora calcularemos el error para cada neurona de salida usando la función del error cuadrada que y dichos resultados los sumaremos por cada neurona para conocer el error total. Veamos, hay que aplicar la siguiente expresión para cada neurona y luego sumar sus resltados.
Eneurona = ½ · (Valorobjetivo – Salida)2
El valor objetivo es el error ideal, es decir, el que deseamos. La “salida” es el valor saliente, después de aplicar la función de activación, de cada neurona.
Etotal = Eneurona 1 + Eneurona 2 + Eneurona 3 +····+ Eneurona n
Vamos a suponer que nuestro valor objetivo para una neurona es 0.01 y para 0.99, es decir, es el valor que nosotros consideramos aceptable. Estos valores los elegimos nosotros y no deben porque coincidir. Entonces:
Eo1 = ½ · (0.01 – 0.75136507)2 = 0,274811084
Eo2 = ½ · (0.99 –0.772870408)2 = 0,023573
Luego el error total:
Etotal = Eo1 + Eo2 = 0,274811084 + 0,023573= 0,298384
El camino inverso
Ahora vamos a actualizar los pesos de la red neuronal para que el error se acerque al deseado y así minimizar el error en cada una las salidas de las neuronas. Vamos a empezar por la neurona de salida. Para ello vamos a emplear la siguiente expresión:
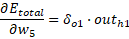
En donde:

Finalmente:
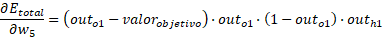
De manera que el nuevo valor del peso será:
En algunos casos, en la literatura, encontraremos “η”, en otros “α” y en otros “ε”. Este valor es la velocidad de aprendizaje. Normalmente se le suele dar 0,5. Sustituyendo con los valores anteriores:
- outh1 = 0,593269992
- outh2 = 0,596282699
- outo1= 0,75136507
- outo2 = 0,772870408
- Valoro1 = 0,01
- Valoro2 = 0,99
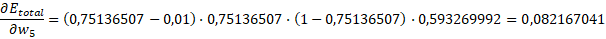
Finalmente el nuevo peso:
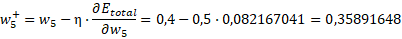
Para los otros casos:
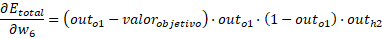
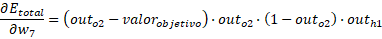
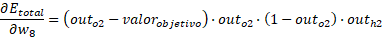
Entonces los pesos hacia la capa de salida son:
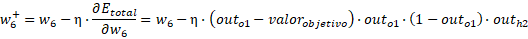
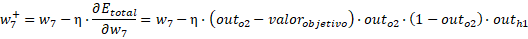
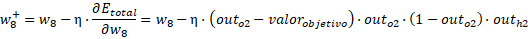
Los valores finales son:
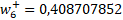
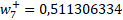
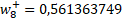
Ahora nos hemos de centrar en los pesos que van desde las entradas a la capa oculta. Para ello usaremos la siguiente expresión en cada nodo:
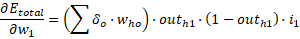
El primer paréntesis es igual a:
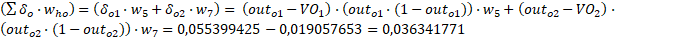
En definitiva:
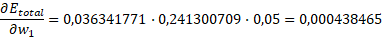
Al final el resultado es:
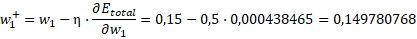
Así con el resto de neuronas. Luego hay que repetir el proceso tantas veces cómo sea necesario hasta llegar al error deseado.
PREDICCIÓN DE SERIES TEMPORALES MEDIANTE REDES NEURONALES
La predicción en las series temporales juega un papel fundamental en, por ejemplo, la economía y en el especial la bolsa (Stock en inglés). La evolución de los precios, puede ser predicho para tomar decisiones. Vamos a emplear el software gratuito Neuroph Studio para ver un caso interesante de predicción de futuros.
Este tipo de predicciones temporales utilizan redes neuronales del tipo perceptrón multicapa (MLP) con el método de back-propagation. En la MLP se suele usar la tangente hiperbólica como función de transferencia.
Para ello tenemos una serie de observaciones x(t-n),.., x(t-3), x(t-2), x(t-1), x(t), que se toman de forma periódica a tiempos regulares. La idea es si conocemos por ejemplo, x(t-3), x(t-2), x(t-1), x(t), ¿qué tendremos en x(t+1)? En inglés este término se denomina por “one step ahead”. Incluso se pueden emplear los datos predichos para calcular futuros más lejanos. Sin embargo, este método, tiene un error acumulativo importante.
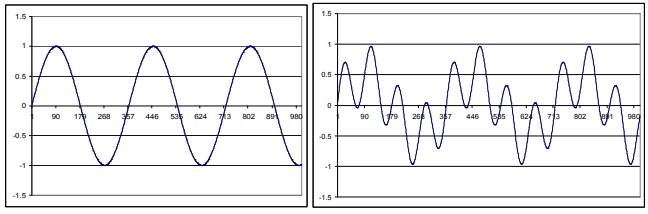
Ahora imaginemos que estamos andando a lo largo de una onda sinusoidal, entonces la pendiente disminuye negativamente y caemos de forma abrupta. Igualmente, cuando lleguemos al fondo del valle (la pendiente crece positivamente) entonces nos toca subir. Entonces de acuerdo de lo preciso que hayas medido las pendientes, sabes cuánto has andado. Pero, ¿con qué precisión y cada cuando debes recordar las pendientes? ¿Cada 5, 15, o 30 pasos?
Pero la cosa se complica con el gráfico de la derecha porque los picos y los valles están a diferente altura.
Supongamos que tenemos datos relativos al coste de un producto cualquiera desde enero del 2008 al octubre del 2009. Vamos a ver como predeciblemente estará el precio de dicho producto en noviembre del 2009 Es decir, un mes después. Para ello primero:
- Establecemos una estrategia: Deseamos que se tengan en cuenta los datos de los cuatro meses anteriores para conseguir los datos del mes siguiente, es decir, del 5 mes. Es decir, sabemos el comportamiento del mercado en los meses de junio, julio, agosto, septiembre y octubre. Con estos datos se hallará el de noviembre.
- Factor de normalización: Se trata de desplazar el punto decimal de acuerdo a esta expresión. normalizedVector[i] = vector[i] / scaleFactor[i]
- Memoria: Es el vector o número de nodos de entrada a la red neuronal. Se denomina por Ninput.
- Frecuencia: El término frecuencia es como de a menudo avanzamos. Es decir, por ejemplo, sólo hemos avanzado 100 pasos pero sólo recordamos sólo el primero, el sexto y el onceavo.
- Número de neuronas ocultas: Una regla es la regla de Baum-Haussler. Esta dice que :

Etolerance es el error que deseamos alcanzar en la red neuronal, que suele ser de 0,01. Ntrain es el número de patrones de entrenamiento. Según el Dr. Valentin Steinhauer otra recomendación más sencilla es que Nhidden = 2·Ninput + 1.
- Tenemos los datos distribuidos mensualmente: Neuroph emplea puntos para separar los decimales de la parte entera. Fijémonos que conocemos el valor de noviembre, pero nosotros lo estimaremos y lo compararemos.
| MES | PRECIO |
| ene-08 | 77.77 |
| feb-08 | 76.85 |
| mar-08 | 77.25 |
| abr-08 | 79.15 |
| may-08 | 81.23 |
| jun-08 | 82.04 |
| jul-08 | 83.46 |
| ago-08 | 85.71 |
| sep-08 | 88.25 |
| oct-08 | 88.42 |
| nov-08 | 88.40 |
| dic-08 | 87.54 |
| ene-09 | 87.02 |
| feb-09 | 87.25 |
| mar-09 | 86.7 |
| abr-09 | 85.73 |
| may-09 | 85.38 |
| jun-09 | 86.96 |
| jul-09 | 88.17 |
| ago-09 | 88.56 |
| sep-09 | 86.77 |
| oct-09 | 82.85 |
| nov-09 | 82.13 |
AJUSTE DE LOS HIPERPARÁMETROS DE UNA RED NEURONAL
El ajuste de los hiperparámetros de una red neuronal, no es más, ni menos que el ajuste de parámetros tales cómo el número de capas ocultas, la función de activación, el número de neuronas de cada capa oculta, la velocidad de aprendizaje y el valor inicial de los pesos.
Hay que intentar reducir al mínimo el número de capas. Una o dos capas es aceptable. Cuantas más capas, más neuronas y más elevado es el tiempo de procesamiento y más necesaria es disponer de un buen equipo para llegar a un resultado. Con cada capa los requisitos de la CPU aumentan enormemente. Luego cuantas más capas, mayor es el número de mínimos locales que aparecen y por tanto mayor la probabilidad que, durante el proceso de entrenamiento, la red neuronal caiga en uno de ellos.
Si hemos de añadir, por el motivo que sea, varias capas hay que intentar realizar una “pirámide”. Esto significa que el número de neuronas de la capa sucesora sea menor que el de la capa predecesora.
- Cuantas más neuronas, la red neuronal es capaz de aprender, pero con mucha más precisión perdiendo capacidad de extrapolación. Esto significa que no es capaz de aprender cosas nuevas. Sube el error de predicción y baja el de aprendizaje. Es decir, de alguna manera pierde capacidad de imaginación. Esto en inglés se conoce como “overfitting”.
- Si hay muy pocas neuronas, la red neuronal no es capaz de aprender. La red se satura. Esto en inglés se conoce como “underfitting”.
Número de capas de neuronas por capa oculta
Una forma de evitar lo anterior se puede empezar con las siguientes reglas aproximadas o consejos.
En el caso de aplicar una capa oculta:
- Número de capas ocultas (hidden): h = (i · o)1/2
- Número de neuronas de la capa de entrada (input): i
- Número de neuronas en la capa de salida (output): o
Entonces una vez aplicado lo anterior, intentamos que el sistema aprenda. Sinó es capaz de aprender, añadimos otra neurona. Así sucesivamente hasta que el sistema sea capa de aprender.
Si al final, esto no funciona, añadimos otra capa oculta, con la siguiente regla:
En el caso de aplicar dos capas ocultas:
- Número de neuronas de la capa oculta 1: h1 = o·r2
- Número de neuronas de la capa oculta 2: h2 = o·r
- Factor r = (i/o)1/3
- Número de neuronas de la capa de entrada (input): i
- Número de neuronas en la capa de salida (output): o
Sino aprende, añadimos otra neurona. Así sucesivamente hasta que el sistema sea capaz de aprender.
Velocidad de aprendizaje o factor alpha
La velocidad de aprendizaje o factor alpha típicos comprenden entre 0.01 a 0.99. El típico es el 0.1. Lo mejor es trabajar con valores pequeños sino la curva de error dará saltos.
Asignación inicial de pesos
Los valores típicos de los pesos sinápticos suelen comprender entre:
- -0.5 < wij < 05
- -1 < wij < 1
- -1/nº pesos < wij <1/nº de pesos
EL MÉTODO DEL GRADIENTE
Este es un algoritmo que se puede emplear en infinidad de campos, para la minimización del error y ajuste de los pesos. La idea es que si la red neuronal aprenda de forma iterativa, es interesante que el valor de los pesos cambie de forma iterativa. Esto se puede expresar como:
w(k) = w(k – 1) + α · f(E)
Necesitamos un método que facilite el cálculo de la derivada del error. Para ello hay varias soluciones. Una es el famoso “Backpropagation” y otra es el método del gradiente. La “backpropagation” es un método que fue muy difundido y muy antiguo. Probablemente este método desaparezca, porque de alguna manera, usa muchos casos/ejemplos para resolver una red neuronal. Luego consume muchísimo.
Es decir, el valor del peso en cada iteración ”k”, es igual al valor del peso en la iteración anterior más un cierto valor proporcional α (factor de aprendizaje) a una función dependiente de la variación del error. Bueno, ¿porque se llama algoritmo del gradiente?
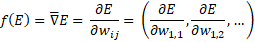
Son derivadas parciales, porque responde a la pregunta: ¿Cómo varía el error si modificamos sólo una de las variables? Al final en cálculo numérico se arregla:
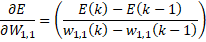
EL “MACHINE LEARNING”
El objetivo del machine learning es que las máquinas aprendan y hasta ahora hemos hablado básicamente del aprendizaje supervisado. Es decir, teníamos unas salidas conocidas, un número concreto de entradas y unos métodos para hallar el valor de los pesos. Es decir, unos métodos para aprender a calcular unos pesos para que a partir de unos valores de entrada obtengamos unas salidas deseadas. Pero no toda la inteligencia artificial funciona así. Vamos a analizar el aprendizaje No Supervisado y el Aprendizaje por Refuerzo.
Aprendizaje supervisado
Como ya hemos indicado anteriormente, el aprendizaje supervisado conoce la solución deseada y esto se denomina “etiquetas” (labels). Un típico ejemplo es el de clasificar un correo electrónico de entrada como no deseado (Spam) o deseado. La idea es definir como correo basura o no, con un 1 o un 0 (un sí o un no). Otro ejemplo típico es el de predecir los valores numéricos. Un caso sería el coste de una vivienda basándonos en sus características típicas (como los metros cuadrados, el número de habitaciones, el tipo calefacción y frío, la distancia al centro urbano, etc.) además deberemos incluir el coste de nuestro conjunto de datos.
Los algoritmos más comunes, conocidos y utilizados en Aprendizaje Supervisado son:
- k-Nearest Neighbors
- Linear Regression
- Logistic Regression
- Support Vector Machines
- Bayesian Classifiers
- Decision Tress and Random Forest
- Neural Networks
- Deep Learning
Aprendizaje No Supervisado
En el aprendizaje No Supervisado los datos de entrenamiento no incluyen las llamadas etiquetas o “labels” y el algoritmo debe clasificar o descifrar las salidas por sí solo. Un ejemplo en el que se usa es el de agrupar la información recopilada de usuarios en una Web o en una aplicación móvil de manera que la IA detecte todas las características que tienen en común.
Los algoritmos más comunes, conocidos y utilizados en Aprendizaje no supervisado son:
- Clustering K-Means
- Principal Component Analysis
- Anomaly Detection
Aprendizaje por Refuerzo
En el aprendizaje por refuerzo la inteligencia artificial actuará con la autonomía necesaria para investigar “un mundo” desconocido y hallar las acciones a realizar mediante prueba y error. La IA aprenderá por sí misma obtendrá premios (también llamadas recompensas) y castigos. Los algoritmos de este tipo de IA crearán la mejor estrategia para conseguir las mayores recompensas posibles en tiempo y forma. Estas estrategias llamadas políticas, delimitarán las acciones a tomar ante cada situación a la que se enfrente. Este tipo de algoritmos se usan para resolver puzles, jugar al Pac-Man o en el Flappy Bird.
Los modelos más utilizados en la actualidad son:
- Los procesos de Decisión de Markov (MDP: Markov Decision Process), es decir, el conocido como Q-Learning.
APLICACIONES DEL MACHINE LEARNING
Hay miles de aplicaciones del machine learning. Desde leer y crear libros de la nada a analizar sólo con un electrocardiograma si pronto morirás aunque aparentemente estés sano.
Básicamente el machine learning se aplica a lo siguiente:
- Reconocimiento de Imágenes
- Reconocimiento de Voz
- Clasificación
- Predicción
- Segmentación de Audiencia
- Juegos
- Coche Autónomo
- Salud
- Economía y Finanzas
- Motores de Recomendación
PASOS PARA CONSTRUIR UNA INTELIGENCIA ARTIFICIAL
Básicamente hay siete pasos a seguir para obtener una inteligencia artificial.
- Recolectar datos
Para implementar cualquier tipo de inteligencia artificial hay que recolectar datos. Estos datos deben ser de calidad porque tiene un impacto directo en el futuro modelo. La cantidad también es importante para generar un patrón correcto y suficiente. También es normal emplear un método conocido como web scraping para recopilar información de automáticamente de diversas fuentes (y/o servicios rest/ APIs). El Web scraping permite obtener datos de páginas web programadas en html. ¿porqué? Muchas webs no permiten extraer contenido clasificado directamente, por lo que el web scraping lo permite hacer directamente.
- Preparar los datos
Es imprescindible mezclar los datos obtenidos puesto que el orden en que se computen los datos dentro del procesador no debe de ser determinante.
También es el momento ideal para observar nuestros datos y comprobar si existen correlaciones entre las distintas características (en inglés “features”). Además, deberemos seleccionar las características, ya que éstas impactarán directamente en el tiempo de ejecución y en los resultados obtenidos. También podremos, si fuera necesario, realizar una reducción de dimensiones aplicando PCA (Principal Component Analysis). La cantidad de datos deberá ser equilibrada, en caso contrario, el aprendizaje podría inclinarse hacia un tipo de respuesta y cuando nuestro modelo intente generalizar lo aprendido fallará. Para ello voy a dar un ejemplo, imaginemos que sólo presentamos a la IA gallinas blancas de todas las formas y tamaños posibles. Una vez entrenado el modelo, al presentarle una gallina negra, probablemente definirá incorrectamente la imagen.
Es importante también separar los datos en dos conjuntos: uno para el entrenamiento y otro para evaluación de nuestro modelo seleccionado. Una proporción típica es des 80/20 pero puede ser diferente según el caso y la cantidad de datos que tengamos.
En esta etapa también podemos procesar previamente nuestros datos normalizando, eliminando duplicidades y corrigiendo errores.
- Elegir el modelo
En este apartado hemos de conocer cuál es nuestro objetivo. No todos los modelos son válidos para cualquier cosa. Veamos la siguiente tabla y sus aplicaciones.
| Modelo | Aplicaciones (Ejemplo de uso) |
| Logistic Regression | Muy utilizado en la predicción de precios de viviendas y terrenos |
| Fully connected networks | Clasificación |
| Convolutional Neural Networks | Procesamiento de imágenes para poder encontrar gatitos en las imágenes. Detección de pornografía. |
| Recurrent Neural Networks | Reconocimiento de Voz |
| Random Forest | Detección de fraude fiscal |
| Reinforcement Learning | Enseñar a la máquina a jugar videojuegos y ganar |
| Generative Models | Creación de imágenes |
| K-means | Permite crear clústeres de datos sin etiquetar. Segmentar audiencias o realizar inventarios |
| k-Nearest Neighbors | Son los motores de recomendación (por similitud/cercanía) |
| Bayesian Clasifiers | Se emplea para la clasificación de correos electrónicos: Spam o no |
- Entrenar nuestra máquina
En este apartado el modelo se implementará y empieza a procesar y recalcular el valor de los pesos.
- Evaluación
En este apartado se verifica la precisión del modelo ya entrenado. Si la exactitud es menor al 50% ese modelo no es válido. Si alcanzamos más de un 90%, podemos tener una confianza en los resultados otorgados. Más de un 70%, se considera un buen modelo.
- Parameter Tuning (sintonización de los parámetros)
Si en el apartado anterior no obtuvimos buenos resultados es posible que tengamos problemas de overfitting o underfitting y deberemos volver a re-entrenar el modelo. Algunas de las cosas que se pueden hacer es variar lo que se conoce como Hiperparámetros (learning rate, momentum, número de neuronas, etc…) además de:
- Revisar los datos de entrada.
- Revisar la cantidad de iteraciones (EPOCH).
- Revisar la tasa de aprendizaje o “learning rate” y el “momentum”.
- Variar el número de capas ocultas.
- Variar el número de neuronas.
- Variar el tipo de activación (relú, sigmoide, etc.)
- Error máximo aceptable.
Es importante no ponerse nervioso y no desesperarse. Este ajuste es un arte y actualmente no está automatizado. Cada modelo tiene sus propios parámetros a ajustar. Esta parte es lenta, que requiere de mucho esfuerzo para lograr unos buenos resultados.
- Predicción e inferencia
Una vez realizado todo lo anterior el modelo posiblemente sea capaz de predecir y de deducir (inferencia) los datos reales que le lleguen de sensores externos. Predecir y deducir no es lo mismo, una predicción es algo que sucede conociendo unos datos de entrada. Es decir, si conoces los datos de entrada vas a conocer unas salidas. Sin embargo, si un coche lleva los cristales mojados podemos deducir que ha llovido.
LOS ALGORITMOS MÁS FRECUENTES EN EL MACHINE LEARNING
Hasta ahora nos hemos centrado en las redes neuronales. Éstas son un tipo de IA, pero no es la única manera de resolver problemas. El machine learning no está relegado sólo a las redes neuronales. Hay otros algoritmos para la resolución de problemas y algunos de los que se suelen repetir con mayor frecuencia son los siguientes:
- Algoritmos de Regresión
- Algoritmos basados en Instancia
- Algoritmos de Árbol de Decisión
- Algoritmos Bayesianos
- Algoritmos de Clustering (agrupación)
- Algoritmos de Redes Neuronales
- Algoritmos de Aprendizaje Profundo
- Algoritmos de Reducción de Dimensión
- Procesamiento del Lenguaje Natural (NLP)
- Otros: Algoritmos de Aprendizaje por Reglas de Asociación, algoritmos de Conjunto, computer Vision, sistemas de recomendación, aprendizaje por refuerzo.
BIBLIOGRAFÍA
Referencias online:
- [1]. https://es.wikipedia.org/wiki/Perceptr%C3%B3n
- [2]. https://mc.ai/backpropagation-in-deep-neural-networks-with-example/
- [3]. http://grupo.us.es/gtocoma/pid/pid10/RedesNeuronales.htm
- [4]. https://es.wikipedia.org/wiki/Neurona
- [5]. Time Series prediction with Feed-Forward Neural Networks -A Beginners Guide and Tutorial for Neuroph Laura E. Carter-Greaves
- [6]. Lógica Difusa – Introducción al Curso y Aplicaciones – Hackeando Tec.
- [7]. Wikipedia lógica difusa: https://es.wikipedia.org/wiki/L%C3%B3gica_difusa
- [8]. Machine Intelligence – Lecture 17 (Fuzzy Logic, Fuzzy Inference): https://www.youtube.com/watch?v=TReelsVxWxg&t=1026s
- [9] https://www.aprendemachinelearning.com/una-sencilla-red-neuronal-en-python-con-keras-y-tensorflow/
- [10]. Programa para la simulación y arquitectura de redes neuronales: http://neuroph.sourceforge.net
- [11]. https://www.youtube.com/channel/UCCmHFfUhcgZHenBWRzSEB0w
- [12]. https://www.youtube.com/channel/UCy5znSnfMsDwaLlROnZ7Qbg
- [13]. https://es.wikipedia.org/wiki/Perceptr%C3%B3n
CONTACTO
Para cualquier consulta no dudes en escribir un comentario. Si necesitas que te ayudemos profesionalmente en el ámbito de la inteligencia artificial, no dudes en contactar con nosotros. También nos puedes ayudar descargando nuestra APP, además de darte a conocer como profesional al mundo.
Autor: Ing. Josep Ramon Vidal Bosch. — Joober Technologies